|
|
 |
|
EXTENDED
PLAY |
|
Why MU?*
Wolfgang
Höhl |
| [in italiano] |
|
|
Introduction
Every liberating
action depends on recognition, which is best performed by scientific methods,so science
becomes the most important instrument for the improvement of our life.
Rudolf Carnap, Intellectual Autobiography
Sir Karl Popper
describes the experiment as an essential part of a four-figure scheme. In this scheme, he
designs a general model for recognition:
01]
The elder problem;
02] Theories as a first trial (= models);
03] Attempt of elimination of models throughout criticism, experimental
proof included;
04] New problems, deriving from the critical discussion of our
theories (1).
One can assume that this four-figure scheme is valid for architecture, as a human product,
as well. Therefore every new building design forms an experimental solution towards a
specific problem, probably with a long history of its own.
To grasp a problem, today we design models or formal systems. There are many abstract
models in architecture: on the one hand we have functional typologies, describing specific
relations of functional areas. On the other hand there are formal typologies for the
composition of various building components. Probably, and not at last, there is a manifold
of constructive solutions and systems. Successful models are improved, less successful
models are critically questioned, adapted or finally removed.
|
|
|
|
Theory is, in any case, the primary basis for amazing actual experience in a
built structure. A rigid formal algorithm forms the basis for an astonishing spatial
adventure in the Viennese Wittgensteinhaus, a clear method and a systematic structure
characterize the up-to-date work "Nested cube in process" of the Japanese
architect Hideyuki Yamashita. The projects of the "Parascape Structure" and the "Hyperstructure of
TransPORT 2001" are recent works of computer controlled environments, based on
functional algorithms. These interactive skins react on the spontaneous actions of all
visitors and are able to adapt their physical form (2). To my mind, we all can be
curious for the finally erected buildings.
Basically there is the fascinating dialectic between a controlled, abstract model and an
experimental interaction with an apparently complex reality.
Important
Dialectics
What is a formal system
and which fascination is it all about this abstract models?
Carnap defines a
constitution system as a "...stepwise order..." of objects, "...so, that
the objects of every level can be constituted form the objects of a lower level. Because
of the transitivity of the reductivity, all objects are constituted from the primary
objects of the first level. These primary objects form the basis of the whole system...
The term "object" is used in a wider sense, for everything which can be
described in a statement" (3). Beside these elements, Carnap describes three
more parts of a constitution system. The description of the quality of elements, the
description of the relation of elements and the description of the structure of the system
(4).
Franz Pichler mentions another essential characteristic. He describes formal systems as
"a construct, which is able to perform a special behavior in an abstract way" (5). With this statement, he confirms the important assumption of a separated
existence of reality and controlled model. By 500 BC, the Greek poet and singer Xenophanes
wrote:
Certain truth no man
ever will discern
About the gods and all things, I talk about.
Should ever one man proclaim perfect truth?
How could he know: everything is filled with suspicion. (6)
In this sense, all our
models and theories are based on more or less reasonable assumptions and rational
construction.
Systems and
Isomorphisms
|

Kas Oosterhuis, Parascape
Structure |
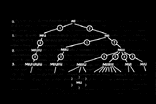
Douglas R. Hofstadter, The MIU-System |
In 1979, Douglas R. Hofstadter designs the so-called MIU-system, in his book
"Gödel, Escher, Bach - an Eternal Golden Braid". In this system he describes a
certain number of sets from the accidentally chosen letters M, I and U. Beginning with the
initial set [MI], this primary set can be deformed by 4 defined rules. From [MI] one will
derive, in the first step and the first rule, [MIU]. In the end Hofstadter derives at the
interesting question, if [MU] can ever be a set of the MIU-system, or not (7).
In the latter example of the pg-system, Hofstadter describes the relations between a
potential set of a constructed system and the interpretation of reality. When we interpret
the following set
- - p - - - g - - - - -
as 2 plus 3 equal 5
so we discover an
isomorphism, between the derived set of a formal system and a part of our own reality.
Hofstadter says:
This is our first
example of the case, that a formal system covers a part of our reality and seems to
reproduce it perfectly, as all sets are isomorphic to the related part in reality. In
spite of that reality and formal system are independent to each other (8).
As an interesting
personal gain Hofstadter describes the discovery of the isomorphism between reality and
the set of a formal system. He mentions this moment as:
...a reason to rejoice.
It appears as a lightning from clear skies and is a source of amazement. The discovery of
an isomorphism between two well known structures means a big heap in knowledge - and I
claim, that these discoveries of isomorphism create meaning in the human brain (9).
An isomorphism can
explain a certain case in reality and give way to successful predictions. Maybe we will
discover more sets in the same system, which might give no sense at all, or have not been
confirmed by evidence yet. These apparently senseless or unconfirmed sets form a valuable
potential for the experimental research and the architectural experiment.
Autocatalytic
Dwellings
Peter Weibel describes
the common use of formal systems in arts and science.
The use of mathematics
and logic models in arts, especially in the analytic and conceptual art forms, is just one
example for the astonishing convergence of science and art (10).
Furthermore Weibel mentions the influence of
abstract models towards modern art, "... far beyond the golden section...",
"...on the way towards abstraction..." (11).
One of the most popular examples for an ideal formal system, is the algorithmic concept
for the Wittgensteinhaus
in Vienna, designed by the philosopher Ludwig Wittgenstein and the architect Paul
Engelmann.
As a design problem Wittgenstein chose the confrontation with an symmetric outward
appearance of all rooms. The self-made simple algorithm "Design all visible surfaces
due to an axis based symmetry" led to a constructive and technological very complex
result, submitting the reasonable architectural syntax for the finish of the surface.
Jan Turnovskı describes in, to my mind, one of the best works on this theme, "Die
Poetik eines Mauervorsprunges" (12), the everlasting problem
between a complex result and a very simple and clear procedure in architecture. This
example not only shows the immense interconnection of architectural reflexivity between
construction, function and form, but belongs to the most fascinating works of the early
20th century.
|
|
|
In 1987, the Graz architect Manfred Wolff-Plottegg makes a solution towards the troublesome design
process in architecture with his "Analogous design generator". The elements of
this machine are pieces of waste, among others made of an accidentally melted foil of a
construction drawing.
Plottegg himself writes:
There is no more
handwriting of the architect as an individual signature, no use for the fulfillment of an
aim, no preformed functions as metaphors of technologies. We have overcome the long-term
dominance of form, object and material; Architecture is no longer a carrier of meaning;
parted from retrospection, free from habits, personal desire and projections, it is no
more an instrument of the powerful. Architecture is no longer derivative, architecture
will be autocatalytic (13).
|

Manfred Wolff-Plottegg,
Analogue Design Generator

Manfred Wolff-Plottegg,
Analogue Design Generator |

Ernst Fuchs, House in Zirl
/ Tyrol

Ernst Fuchs, House in Zirl
/ Tyrol

Ernst Fuchs, House in Zirl
/ Tyrol |
1996 Ernst J. Fuchs, member of the Viennese Group "The POOR BOY's
ENTERPRISE", presents a design for his autocatalytic dwelling. He develops a
spatial structure for a single family dwelling in Zirl / the Tyrol from the framework of
the existing conditions on site. As a "spatial data field", these factors will
initiate a generative process for the final form of the building.
After a few program loops, a sunny and multiple formed object developed on manifold
pillars from the ground, which laid mainly in the shadow.
The recent project "nested cube in process" of the Japanese architect Hideyuki Yamashita
develops as a self-reflexive spatial sequence from the mathematical set of the Euler
Theorem. The architect bases the concept of the building on the so called
"re-normation of space". This, she calls a constant relation between the
corners, edges, and surfaces of an Euclidean body.
In a simple polyhedron,
the sum from the amount of corners and surfaces is equal 2 + the amount of all edges (14)
N corners + N surfaces
- N edges = 2
Probably the architect
develops a condition for balance between the corners, edges and surfaces and defines the
new outline of her building. In this case the object is just one of all possible forms,
with an equal amount of surfaces, edges and corners.
This self-reflexive interconnection is made visible by an optical design concept. Mirrors
in the central area give always a view of a strolling visitor throughout the whole
building, and even towards the outside.
The basic room is being
wrapped from the other rooms and wraps the other rooms in itself (15).
4-D Variations
Have we been confronted
with positive and negative form, functional areas or constructive components as elements
in various formal systems, Wittgenstein chose a self-reflexive geometry as a constituent
of his composition. Pieces of waste are the elements of the design generator, a defined
amount of site-conditions form the basis of the autocatalytic design of Ernst J. Fuchs, a
simple mathematics theorem forms a variety of possible geometries in the nested cube
project of Hideyuki Yamashita.
"How free is freedom", Otl Aicher asked himself and described the delicate
relations between the improbable freedom in the possibilities of a soccer match and the
systematic order of the necessary rules.
Freedom presupposes the
order, they are related to each other, one is founded on the other (16).
In any of the projects
mentioned, there emerges an enormous amount of variations in a rigid framework of
conditions. Some of the variations might be useful in handling a topical problem, others
might be less useful, some complete senseless, but still possible.
These enormous possibilities will always be in the center of a sensible application, as
operable tools in the computer aided design process and the experimental design, with
surprising results and a fantastic potential of surrealistic interpretations.
4-D, Buckminster Fuller named a series of designs in the time about 1928. It stood for
"four-dimensional thinking - thinking in time instead of only in space, thinking of
consequences for humanity instead of only immediate personal gain" (17). In this way, he defines design as a necessary and contemporary solution for the
improvement of our circumstances.
The computer aided design process today, opens a broad field of possibilities in the
application and the automation of self-generating algorithms. Just in this point formal
systems stay commonly understandable and open for a surprising architectural and cultural
experiment.
Most interesting will be an integral solution towards architectural design problems, not
only oriented at the final form of a building, but respecting all necessary data.
|
|

|
|
Notes
(1) Karl R. Popper, "Alles Leben ist Problemlösen", München 1997, p. 32.
(2) Ole Bouman, "Quick Space in Real Time", Part 3, in "Archis",
6, 1998, p. 72.
(3) Rudolf Carnap, "Der logische Aufbau der Welt", Hamburg 1979, p. 1.
(4) Rudolf Carnap, 1979.
(5) Franz Pichler, "Mathematische Systemtheorie", Berlin 1975, p. 13.
(6) Karl R. Popper, "Auf der Suche nach einer besseren Welt", München
1987, p. 50.
(7) Douglas R. Hofstadter, "Gödel, Escher e Bach", Stuttgart 1985, p. 37.
(8) Douglas R. Hofstadter, 1985, p. 58.
(9) Douglas R. Hofstadter, 1985, p. 54.
(10) Peter Weibel, "Analyse des Realen", in "Jenseits von Kunst",
Neue Galerie Graz 1998, p. 48.
(11) Peter Weibel, 1998.
(12) Jan Turnovskı, "Die Poetik eines Mauervorsprunges", Braunschweig
1999.
(13) Manfred Wolff-Plottegg, "Architektur Algorithmen", in Peter Weibel,
"Jenseits von Kunst", Wien 1997, p. 704.
(14) Karl Kreutzer, "Mathematik", München 1969, p. 198.
(15) "Die Schrift des Raumes", Kunsthalle Wien 1996, p. 82.
(16) Otl Aicher, "Typografie", Lüdenscheid 1992, p. 15.
(17) Martin Pawley, "Buckminster Fuller", New York 1990, p. 39. |
|
 |

|
|
Back to: EXTENDED PLAY |
|
 |
|
laboratorio
informa
scaffale
servizi
in rete

|






