|
|
||||
| home > extended play | ||||
| Verso
un modo di produzione non-standard Patrick Beaucé, Bernard Cache (Objectile) |
||||
| Il
seguente testo di Bernard Cache e Patrick Beaucé è stato composto in
occasione della partecipazione del gruppo Objectile alla mostra Non-Standard
Architecture, inauguratasi al centro Georges Pompidou lo scorso
10 dicembre e visitabile fino al 1 marzo 2004. Un commento sulla mostra
è disponibile all'interno di ARCH'IT nella sezione Sopralluoghi. Il testo, che qui riportiamo nella sua versione integrale datata 17 marzo 2003, era stato originariamente concepito per apparire all'interno del catalogo che accompagna l'esposizione, dove compare in versione notevolmente ridotta, con ampi tagli che coinvolgono tutta la parte iniziale e prevalentemente teorica. Così facendo, i curatori del catalogo hanno messo in risalto gli aspetti della trattazione più legati alla pratica (della produzione con metodologie non-standard) tralasciando, soprattutto per motivi di spazio, la struttura teorica che sostiene le scelte progettuali e costruttive del gruppo Objectile. Ma è proprio questa struttura teorica che qui ci interessa divulgare, poiché si inserisce all'interno di una ricerca più ampia riguardante i concetti di forma e di geometria, che il gruppo di Cache e Beaucé sta sviluppando ormai da diversi anni. A questo proposito è possibile consultare un altro loro testo, di qualche anno antecedente, intitolato In difesa di Euclide e pubblicato da ARCH'IT in questa stessa sezione. La visione del gruppo Objectile ci affascina per la sua capacità di risalire alle origini della geometria e della filosofia e riscriverne la storia, in una nuova declinazione, in cui le due discipline si intrecciano seguendo un unico sviluppo che porta tutto d'un fiato fino all'utilizzo delle tecnologie non-standard, viste qui come una normale conseguenza dell'evoluzione del pensiero scientifico e della tecnica. [Teresanna Donà teresanna@libero.it] |
|
|||
| A
quali condizioni un'espressione come "architettura non-standard" può
avere senso? Forse è più facile cominciare a rispondere per negazioni.
Se in effetti un'architettura non-standard consistesse nel generare
delle superfici più o meno morbide che definiremo in seguito come edifici
trasferendoli su una batteria di software di produzione, per creare
delle specie di sculture a prezzo molto elevato che non hanno più alcun
rapporto con la sedimentazione storica e sociale che costituisce la
città, allora non faremmo che perpetuare il mito romantico dell'architetto
artista. Al di là di ogni intenzione polemica, questo esordio negativo ci deve servire per enunciare una serie di criteri ai quali noi desidereremmo tentare di rispondere positivamente, per non farci sfuggire ciò che è davvero in gioco nella possibilità di un'architettura non-standard al giorno d'oggi. È una questione di forma, di città e di produttività. |
[14feb2004]
|
|||
| Iniziamo
con la forma poiché, non neghiamolo, essa ha un certo "fascino". E in
effetti, uno straordinario sentimento di potenza invade ogni architetto
cui i modellatori CAD (1) danno la possibilità di generare delle superfici
che altrimenti non saprebbe assolutamente disegnare con riga e squadra.
A questo proposito possiamo considerare tre casi. Il sentimento di totale
potenza può venire in primo luogo dai modellatori estremamente ergonomici,
come Rhino, che permettono di disegnare in maniera molto facile delle
superfici sufficientemente complesse da non essere nemmeno più certi
della loro coerenza spaziale. Il grande pubblico non ne ha ancora la
più pallida idea, ma "tirare" i punti di controllo di una superficie
NURBS per dare origine ad una superficie fluida è oramai alla portata
di un qualunque utilizzatore dopo solo una mezz'ora di apprendimento.
Che d'altro canto si tratti poi di controllare queste superfici, di
modificarle agendo sulle loro quote, di conferire loro uno spessore
e di fabbricarle, questo è un altro paio di maniche e lì comincia il
gioco del gatto e del topo: cioè trasmettere i problemi a qualcun altro
e moltiplicare il preventivo. Di qui l'adagio, molte volte ripetuto
da architetti lucidi come Alejandro Zaera Polo: nulla viene costruito
che non sia trasferibile su Autocad. Secondo caso: l'utilizzo di generatori complessi, come i simulatori di movimento di particelle che troviamo in software come Maya, Softimage e altri programmi che non sono assolutamente criticabili in sé, ma che non sono mai stati pensati per fabbricare degli oggetti concreti, e che dunque non si preoccupano affatto di assicurare, ad esempio, che i quattro spigoli di un'asse siano complanari. Nel primo caso, il fascino derivava dalla semplicità di un'interfaccia molto trasparente, in questo secondo caso il fascino proviene dal fatto di disporre, al contrario, di motori talmente complessi da non riuscir più a controllare il dispositivo di generazione, cosicché il risultato ci arriva rivestito da un manto di innocenza: quello della casualità e dell'incidentalità. Di fatto questo caos è interamente determinista, ma dal momento che non ne comprendiamo i determinanti algoritmici, le forme sono contraddistinte da una sorta di aura conferita da una finta aleatorietà. |
||||
| Infine
c'è un terzo caso, molto più onesto, che consiste nel fare a meno della
scatola nera informatica, per torcere semplicemente dei fogli di carta,
come un buon vecchio bozzetto di scultura, procedimento che ha il vantaggio
di creare delle superfici "di sviluppo", cioè a curvatura nulla, il
che vuol dire che queste superfici sono intrinsecamente euclidee. (2)
Bisognerà allora digitalizzare il modello di carta, per trasferirlo
su un programma in grado di regolarizzare le superfici, prima di fornire
i files a delle imprese virtuose del prêt à porter architettonico,
come la Permasteelisa. (3) Nei tre casi, il "non-standard" torna a significare "originale" o "complesso", ma, comunque, non riusciamo ad uscire da uno spirito Beaux-Arts, che vuol fare del progetto d'architettura un'opera di creazione individuale. E da questo punto di vista, l'architettura non-standard si inscrive in una tradizione dell'unicum, trasversale a tutti i modi di produzione: artigianale, artistico, industriale o digitale. Il punto di vista alternativo è la serie: l'oggetto come istanza in un continuum. Ma anche qui si richiedono delle precisazioni. Poiché sappiamo bene che oggi, grazie alla magia delle funzioni del morphing, tutto può essere trasformato in tutto. A voler evitare il vortice dell'unicum, ci si sfracella immediatamente sullo scoglio delle trasformazioni senza consistenza propria, che garantiscono una continuità artificiale tra forme che non hanno alcun rapporto tra di loro. |
||||
| Nel
1810 il matematico Brianchon inventa un teorema che si deduce dal teorema
di Pascal attraverso una semplice permutazione dei termini del suo enunciato
(ad esempio, sostituendo alla parola "punto" la parola "retta" e viceversa).
Nel caso classico, il teorema di Brianchon appare quasi come una banalità
poiché enuncia che le diagonali di un poligono regolare si incrociano
al centro del cerchio inscritto; caso tipico di una pianta centrale
del Rinascimento. Il fatto interessante è che questa proprietà si conserva
qualunque sia il poligono inscritto in una qualunque conica, che si
tratti di un poligono convesso inscritto in un'ellisse (figura 2), o
di un poligono incrociato sempre all'interno di un'ellisse (figura 3).
Questa proprietà si applica dunque ad una varietà molto più estesa dell'architettura
classica. D'altro canto questa proprietà non è più utilizzabile nel
momento in cui la conica inscritta degenera in una coppia di rette. Il teorema di Pascal è complementare a quello di Brianchon in quanto a validità all'interno dei casi estremi: classico e degenere. Pascal enunciava che le coppie di lati opposti di ogni poligono inscritto all'interno di una conica si incrociano in tre punti allineati; proprietà duplice che appare chiaramente nella figura 2 e che si conserva nel caso di un poligono incrociato come quello di figura 3. Secondo Pascal la conica può anche degenerare in una coppia di rette, ottenendo così il buon vecchio teorema di Pappo (figura 4). Invece, il teorema di Pascal non è più rappresentabile nel caso in cui la conica si trasformi in un semplice cerchio (figura 1): la retta passa allora all'infinito. Precisiamo che questo teorema fu enunciato nel 1639, ben prima che Pascal entrasse in rapporti con Port Royal. 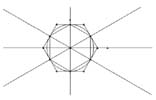 1. Il teorema di Brianchon in una presentazione classica (Pascal non è qui rappresentabile). 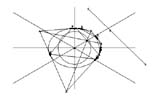 2. Una leggera deformazione che permette di rappresentare entrambi i teoremi.  3. Una forte deformazione che rende i due teoremi irriconoscibili. 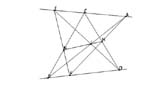 4. Una degenerazione che supporta solo il teorema di Pascal: si ottiene così il teorema di Pappo. |
Morphè,
precisamente. Che cos'è una forma? Che cosa devono avere in comune
due oggetti affinché si possa dire che hanno la stessa forma? La risposta
risiede in un concetto fondamentale della teoria architettonica, ma
ugualmente dell'assiomatica moderna della geometria come formulata
da Hilbert nei suoi Grundlage der Geometrie. (4) Due oggetti
hanno la stessa forma nel momento in cui, indipendentemente dalle
loro dimensioni, gli elementi che li compongono formano tra loro gli
stessi angoli, e soprattutto rispettano le stesse proporzioni.
Questo termine ha perso parte della sua forza: la preoccupazione della
forma prende nutrimento da una teoria delle proporzioni che bisogna
capire a fondo se si vogliono evitare gli scogli che hanno troppo
di frequente costretto il procedere del pensiero architettonico, a
partire dall'acustica neo-pitagorica fino al Modulor di Le Corbusier.
Ora, il filosofo che pone il problema in maniera più chiara, e qui
in relazione all'architettura, è sicuramente Platone nel suo Sofista. |
|||
| Ma
ritorniamo a Platone, il quale riconosce la fondatezza delle correzioni
ottiche. Non nega agli artisti le ragioni per attentare al modello,
quello che rimette in causa è il risultato. Una statua collocata in
cima ad una colonna deve essere deformata, ma questa copia dalle proporzioni
alterate è il prototipo stesso dei simulacri che Platone discredita.
Il fatto è che, rispetto alla matematica del suo tempo, Platone non
ha i mezzi per concepire delle Idee che restino invarianti mediante
deformazione proiettiva. Per vederci qualcosa che non fosse corruzione,
bisognava che Platone avesse a disposizione le invarianze proiettive,
e in particolare quel rapporto del rapporto, quel logos al secondo
grado, che i matematici spagnoli chiamano in maniera molto azzeccata
"razon doble", una locuzione che esprime la quantità di ciò che si conserva
nelle deformazioni proiettive. Vediamo come procede il discorso scientifico.
Il primo tipo di invarianza è il rapporto di identità, rapporto isometrico
da uno stesso allo stesso. Poi troviamo un secondo tipo di invarianza,
un'invarianza per variazione che articola la razionalità greca
e dalla quale non usciamo fino al 1638, per lo meno per ciò che riguarda
la sua traduzione nello spazio geometrico: il rapporto omotetico. Là
interviene Desargues, seguito da vicino da Pascal, i quali creano le
prime invarianze proiettive geometriche: allineamento e intersezione,
prima che venga inventato il birapporto numerico. Dopo Desargues, ci
vorranno appena dodici anni perché Eulero produca, nel 1736, le prime
invarianze topologiche che sono conservate attraverso ogni deformazione
delle superfici, fintanto che ne rispettiamo la continuità. La famosa
formula di Eulero che stabilisce che la somma del numero dei vertici
di un poliedro, aumentata del numero delle facce e diminuita del numero
degli spigoli, rimane costante per qualunque poliedro, questa formula
costituisce la prima invarianza topologica, a partire dalla quale si
è aperto un campo d'investigazione che è ancora in atto poiché, per
esempio, la teoria delle invarianze caratterizzanti i nodi costituisce
un soggetto di ricerca estremamente attivo al cospetto delle matematiche
contemporanee. Ma è a partire dal 1872, grazie a Félix Klein (6), più
conosciuto per la sua bottiglia, che sarà scelto questo movimento della
ragione geometrica che progredisce inventando delle invarianze sempre
più sofisticate per permetterci di manipolare delle variazioni sempre
più estese. Che rapporto può dunque avere questa breve scorsa storica nel campo della geometria con le occasioni da non perdere, oggi, di creare un'autentica architettura non-standard? Quale rapporto dunque tanto con l'architettura che con il non-standard? Noi ricorderemo dell'architettura una definizione tutto sommato estremamente classica: ordinare le diversità dello spazio in modo da assicurare il massimo di libertà alla collettività che lo abita e lo colonizza. Ordinare significherà munire di invarianza un diverso che non è per natura vivibile. Lo spazio assoluto è un esterno che non è tanto più abitabile dell'iper-griglia di un'architettura totalitaria. Noi cerchiamo dei dispositivi, i più flessibili possibile, che assicurino le invarianze necessarie alle varietà. È in questo che ci riporta all'architettura non-standard, alla quale noi riteniamo che le tecnologie digitali potrebbero permettere di varcare una soglia, senza che la nozione sia in sé realmente nuova. Poiché, in effetti, se lasciamo da parte quelle forme estreme che hanno potuto originare delle architetture dalle invarianze isometriche come il cenotafio di Newton o gli spazi concentrativi di un Hilberseimer, il pensiero architettonico si è sempre rivolto prioritariamente verso le invarianze proporzionali. Al punto che un Le Corbusier si rimette ancora alle proporzioni nel momento in cui tenta di elaborare un sistema universale di standardizzazione industriale. Che egli invochi poi una concezione armonica e neo-pitagorica inventata interamente da degli ideologi tedeschi del XIX secolo (7), non toglie nulla alla pertinenza del concetto di proporzione in architettura; ben al contrario, questo fuorviamento moderno prova fino a che punto è difficile pensare l'architettura senza la proporzione. Quindi, quando i teorici del Rinascimento italiano si sforzeranno di interpretare il dispositivo prospettico inventato da Brunelleschi nel 1420, è ancora e sempre al sistema delle proporzione che faranno ricorso, sforzandosi, invano, di appiattire il dispositivo proiettivo sulla similitudine, stabilendo dei rapporti semplici tra i segmenti in diminuzione di un pavimento lastricato visto in prospettiva, quando si tratta invece di un caso canonico di birapporto proiettivo. Il fatto è che l'architettura intratterrà con la proiezione rapporti sempre estremamente ambigui. Quand'anche la geometria proiettiva fu preparata e infine inventata da architetti: una filiazione che si estende per duecento anni, da Brunelleschi a Desargues passando per Philibert De L'Orme, prolungandosi almeno fino a Monge di cui il primo campo di applicazione furono le fortificazioni militari all'Ecole Mézières, quand'anche furono dunque degli architetti ad aver concepito la proiezione, le opere stereotomiche che integrano questa geometria all'interno della produzione architettonica sono sempre restate secondarie: tutt'al più delle magnifiche volte come nell'edificio comunale di Arles (8), ma più spesso delle singole aggiunte, come le trombe di Philibert De L'Orme. E le invarianze topologiche, come gli intrecci, si presentano sotto una circostanza ancor più problematica: il groviglio (9) o l'intreccio vegetale (10) che gioca il ruolo di motivo fondamentale dell'ornamentazione, registro dal quale, prima dei progetti contemporanei, queste forme topologiche non sono quasi mai uscite, eccetto nel caso di qualche applicazione particolare come gli straordinari dispositivi di scale tipo quello realizzato da Philibert De L'Orme per il Castello delle Tuileries (11). Questa analisi formale richiede certo maggiori precisazioni, ma più consideriamo la storia dell'architettura sotto l'angolo delle tecnologie CAD-CAM (12), più è evidente che la tradizione ha sempre integrato, anche se con dosaggi molto diversi, questi quattro tipi di invarianze: isometriche, omotetiche, proiettive e topologiche. Ciò che accade oggi è che noi disponiamo di mezzi che permetterebbero di rimettere in causa il sistema di gerarchie implicito in questi diversi registri, in favore oramai delle invarianze più sofisticate: proiettive e topologiche. Ma noi non crediamo certo di più a un'architettura solo topologica (aleatoria, fluida, in movimento o virtuale, per non dire non-euclidea o chissà cos'altro ancora) di quanto non diffidiamo di un'architettura isometrica (centrale, ortogonale e panottica). Noi siamo tanto più alla ricerca di una giusta e ordinaria via di mezzo che integri i differenti registri di invarianze, quanto più il consenso mediatico si sposta ai giorni nostri sempre maggiormente a favore delle ernie spaziali in qualche sito privilegiato, per non lasciare altro che maggiore estensione all'alternanza griglia/caos nelle periferie. In linea di massima, e al di fuori di situazioni in cui certe invarianze sono date dal contesto stesso dell'edificio, l'architettura saprà ordinare tanto meglio le diversità spaziali quanto più maneggerà ciascuna delle quattro invarianze deterritorializzando il loro registro di applicazione tradizionale: isometria delle piante centrali, omotetia di un'architettura proporzionale, proiettività dei solidi complessi e topologia degli ornamenti intrecciati. Questa reinterpretazione dei registri tradizionali passa attraverso una rilettura delle tipologie urbane storiche. Un'architettura fondata su delle invarianze per variazione permette infatti di recuperare la tipologia in maniera diversa che sotto il modo neo-platonico (13) del modello da riprodurre, in modo identico o seguendone le proporzioni (14). La città diventa allora il campo di variazione delle invarianze storiche. |
||||
| Più
precisamente, essendo le relazioni all'interno della città almeno in
parte determinate dai rapporti di produzione, come fare affinché un'architettura
non-standard diventi un fatto sociale che non sia semplicemente l'ultima
forma di distinzione di una clientela che ha i mezzi di moltiplicare
i preventivi standard? Come evitare che il non-standard non sprofondi
nel formalismo originale? Come fare affinché l'oggetto sia davvero concepito
e prodotto come un'istanza in una serie? Come integrare l'oggetto architettonico
nel tessuto urbano? A tutte queste domande c'è, a nostro avviso, una
risposta fondamentale: la produttività degli studi di architettura,
dalla concezione alla fabbricazione. Da questo punto di vista, la questione
dell'architettura non-standard non è diversa da quel problema fondamentale
delle società post-industriali, vale a dire la produttività dei servizi
in generale (15). L'architetto è un lavoratore intellettuale il cui
modo di produrre è condizionato dalle tecnologie digitali, ma lo sviluppo
di queste non ha nulla di naturale. A questo proposito, la scrittura
di software è contemporaneamente il genere letterario principale della
cultura contemporanea e il terreno privilegiato sul quale si affrontano
le forze che organizzano la produzione nelle nostre società. In questo
campo ritroviamo un concetto strategico che determinerà la forma che
prenderà l'architettura standard nei prossimi anni: è il concetto di
associatività. Che cosa intendiamo per associatività? L'associatività è il metodo che, tramite l'utilizzo di un software, permette di costituire il progetto architettonico attraverso una lunga catena di relazioni, dalle prime ipotesi concettuali fino alla guida delle macchine che prefabbricano i componenti da assemblare in cantiere. Disegnare con un software associativo equivale a trasformare il disegno geometrico in un'interfaccia di linguaggio di programmazione. Così, creare un punto all'incrocio di due linee non consiste più nel creare un elemento grafico, ma nello stabilire una relazione di intersezione sulla base di due relazioni di allineamento. Qui, il lettore si ricorderà delle due invarianti proiettive fondamentali, che sono nello stesso tempo i due gesti primitivi nello spazio: guardare e intercettare. I software di CAD-CAM associativo si occupano di tradurre questa relazione geometrica in un programma che farà in modo che il punto di intersezione si ricalcoli a dovere quando spostiamo i punti di estremità dei segmenti delle rette che intersechiamo. Ben inteso, qui non si tratta che di un anello elementare della catena, e tutto questo diviene interessante in campo architettonico solo a condizione di poter costituire delle lunghe catene di dipendenze, sulla base di un piccolo numero di elementi primitivi che denomineremo, in gergo tecnico, dei "genitori originari". Prima conseguenza, dunque, dell'associatività: l'obbligo di formalizzare razionalmente il progetto architettonico, prendendo ben cura di distinguere antecedenti e dipendenti, col rischio altrimenti di creare dei riferimenti circolari o altri tipi di incongruenze logiche. L'associatività costituisce dunque un filtro che obbliga a pensare in maniera razionale il progetto di architettura e ad esplicitarne le ipotesi. Dopo un certo periodo questo dovrebbe favorire la chiarezza delle procedure e dei concetti architettonici. Tanto che possiamo stupirci del fatto che questo metodo abbia riscosso così poco interesse presso coloro che si mostravano un tempo fiduciosi in un'architettura razionale. Ciò che abbiamo appena descritto riguarda solamente le attività di concezione del progetto. Ora tutta la difficoltà dell'architettura non-standard sta nella grande quantità di informazioni che bisogna generare e manipolare per fabbricare industrialmente dei componenti diversi gli uni dagli altri, ad un prezzo che non sia necessariamente più elevato di quello che si otterrebbe con un procedimento standard. Per generare efficacemente questi flussi di informazioni e assicurare un'associatività completa tra concezione e fabbricazione, è importante prima di tutto lavorare su uno stesso nucleo, che permetterà, tra l'altro, di assicurare il controllo dimensionale dei componenti dalla fase di concezione fino alla generazione dei programmi (codice ISO) che muoveranno le macchine digitali assicurando la produzione degli oggetti. In questo modo, il capitolato di un sistema di CAD-CAM associativo comprende almeno quattro elementi fondamentali. Il primo ha per causa la necessità di gestire dei grossi insiemi di elementi complessi e tutti diversi, elementi che non è più possibile disegnare uno per uno. Questo obbliga a ricorrere ad un processo che chiamiamo tecnicamente l'inserzione dei componenti. Il disegno di un progetto per inserzione di componenti obbliga a concepire innanzitutto un "modello" di relazioni che deve essere possibile applicare in tutte le situazioni in cui bisognerà creare un componente dello stesso tipo. Il modello è in qualche modo un'invarianza che deve supportare tutte le variazioni alle quali saranno sottoposti i termini entro cui avremo stabilito delle relazioni. Che il platonismo porti in germe tutti gli sviluppi tecnologici delle nostre società occidentali, questa è per noi un'affermazione che non è più oggetto di speculazione teorica, bensì il risultato di verifiche empiriche. E noi in effetti abbiamo potuto sperimentare delle situazioni in cui l'implementazione di questa logica di componenti in un progetto non-standard ha potuto generare dei guadagni di produttività di un fattore 100!! D'altronde non è che alla condizione di guadagni produttivi di questo ordine di grandezza che l'espressione "architettura non-standard" prende senso. |
||||
| Gli
altri aspetti del capitolato sono: la necessità di lavorare in flusso
continuo, in uno stato di informazione provvisoria fino all'ultimo momento
ed in modo delocalizzato. Moholy Nagy sosteneva già negli anni ‘20 del
‘900 che il criterio di modernità di un lavoro fosse la capacità di
essere trasmissibile per telefono. Questo è particolarmente vero oggi.
La molteplicità e la dispersione degli interlocutori, la volatilità
delle decisioni, obbligano a cominciare a formalizzare il progetto sulla
base di un'informazione incerta. Alcuni valori devono poter essere dati
per default e in seguito potranno facilmente essere corretti.
Dei punti devono poter essere definiti in un luogo geometrico senza
ricevere delle localizzazioni definitive in questo luogo, i programmi
di fabbricazione devono poter essere aggiornati la vigilia della loro
esecuzione. Prima di prendere la forma di edificio costruito, l'architettura
non-standard procede dunque da un'architettura astratta che ordina i
flussi di informazioni necessari alla produzione digitale e qui in maniera
talmente automatizzata da non prevedere più intermediari tra il progettista
e la macchina. La modifica di uno dei "parenti originari" del progetto
deve provocare l'aggiornamento automatico dell'integralità della catena
informatica, poiché l'intervento umano è sempre soggetto ad errori.
Ora un'architettura realmente non standard potrà davvero nascere solo
a condizione di riuscire a riprodurre nel campo della costruzione ciò
che è già avvenuto nel campo dell'editoria. Come oggi è possibile scrivere
ed impaginare dei documenti grafici che possono poi essere messi in
Internet dal loro ideatore, per poter essere stampati a richiesta da
un lettore distante, l'architettura non-standard presuppone che l'ideatore
di un edificio sia capace di produrre l'integralità dei documenti necessari
alla produzione distante dei componenti architettonici senza intervento
a posteriori di alcun ufficio di controllo o di ingegneria che ne filtri
gli errori. Infine, affinché tutto ciò non resti allo stadio utopico,
questa catena informatica automatizzata deve comprendere i documenti
che servono da supporto alle transazioni economiche necessarie alla
produzione del costruito: descrizioni, preventivi, ordini di produzione
e di consegna, piani di montaggio, ecc. Evidentemente tutti questi elementi del capitolato fanno dell'associatività un dispositivo contemporaneamente molto potente e complesso. I software di CAD-CAM hanno oggi appena iniziato a mettere in opera una tale architettura informatizzata in campi come la meccanica. Ma nulla ci assicura che questa associatività completa sbocci al di fuori di applicazioni industriali estremamente particellari e delimitate. Alla fonte ci possono essere svariate ragioni di ordine sociale, giuridico e culturale, che potremmo riassumere in un'unica formula: affinché l'associatività non sia soltanto una prodezza tecnologica e affinché questa si inscriva nella realtà economica, bisogna assicurare una forte integrazione tra concezione e produzione. A cosa serve in effetti sviluppare degli strumenti di calcolo molto sofisticati se non si trovano poi degli utilizzatori –e in particolare degli architetti– disponibili a comprenderne il funzionamento? La competenza e il rigore necessari all'utilizzo di questi software fa si che essi siano naturalmente destinati ad utilizzatori ben formati e dotati di buone capacità di ragionamento logico e geometrico. A cosa serve ugualmente sviluppare un'associatività tra concezione e fabbricazione se, nella pratica, chi richiede i prodotti e i produttori che li forniscono non giungono a stabilire delle relazioni che permettano di sfruttare positivamente la continuità del flusso di informazioni? Fintanto che ciascuna delle due parti non troverà una sistemazione che le metta in grado di trarre vantaggio dalla collaborazione e di non interrompere artificialmente questa catena rigettando la responsabilità sull'altra parte, l'associatività non sarà che un argomento di marketing per gli editori di programmi o peggio ancora, un errore strategico di sviluppo. Più che mai, l'architettura non approfitterà delle opportunità offerte dal non-standard, se non a condizione di costruire, progressivamente e pazientemente, una vera cultura della produzione digitale. Patrick Beaucé, Bernard Cache (Objectile) |
||||
| Traduzione di Teresanna Donà. | ||||
| NOTE: 1. Computer Aided Design. 2. Su tutte le superfici sviluppabili su un piano, la somma degli angoli di un triangolo resta costante e uguale a 180°. 3. Impresa italiana, leader sul mercato dei rivestimenti di facciata per immobili di grandi dimensioni e di forma irregolare. 4. David Hilbert: Fondements de la géométrie (1899): vedere il capitolo dedicato alla teoria delle proporzioni. 5. Ci sembra importante far notare che il teorema dell'esagono mistico fu inventato ben prima che Pascal si legasse a Port-Royal. Ci sarebbe dunque un cammino mistico proprio di Pascal che non avrebbe niente a che vedere con le relazioni con la sorella, e la sua entrata in convento. Guarini, che rigettò le implicazioni laiche della geometria arguesiana, ne era forse a conoscenza? 6. Félix Klein esporrà i propri concetti generali di geometria nei due testi seguenti: Über die so-genannt Nicht Euklidisch Geometrie (1871) avente come soggetto le geometrie dette non-euclidee. Erlangen's programm (1872): Programma di Erlangen. 7. Le nombre d'or, anatomie d'un mythe. 8. Costruito probabilmente da Hardouin-Mansart attorno al 1640. 9. Gottfried Semper, Der Stil, 1861. 10. Alois Riegl, Stilfragen, (1893); trad. francese: Questions de style, 1992, Hazan. 11. Vedere il disegno di ricostruzione in Philippe Potié: Philibert De L'Orme. Figures du projet. 12. Computer Aided Design e Computer Aided Manufacturing: concezione e produzione con l'ausilio dall'elaboratore. 13. A livello dei problemi, la filosofia platonica ci sembra ben più aperta che la maggior parte delle interpretazioni date dagli epigoni. 14. Vedere la serie di illustrazioni in cui un esagono regolare, archetipo di pianta centrale, viene progressivamente trasformato in una figura che alcuni architetti californiani di certo non rinnegherebbero, pur conservando le invarianze proiettive dei teoremi di Brianchon e di Pascal: convergenza delle diagonali e allineamento delle intersezioni dei lati opposti. 15. Paul Krugmann: L'âge del rendements décroissants, Economica, e La mondialisation n'est pas coupable; vertus et limites du libre échange, La Découverte. Più congiunturalmente, ci si può riferire all'articolo di Patrick Artus nella rubrica «Economiques» di Rebonds del giornale Libération del 31 marzo 2003, dal titolo: "Des finances pour la croissance de l'Europe". 16. Non possiamo che rendere qui omaggio a coloro che si occupano dello sviluppo del programma Top Solid, all'interno della società Missler, e che giorno dopo giorno lavorano a questo software su cui si basano le applicazioni di Objectile. Ringraziamo qui Christian Arber e Jean-Luc Rolland e con loro tutto il gruppo di collaboratori, tra i quali non mancheremo di ricordare Jean-Louis Jammot e Charles Claeys. |
||||
|
Per
qualsiasi comunicazione laboratorio
|